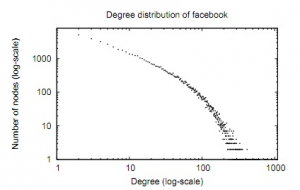
In 1999, it is discovered that almost real large-scale networks follow the same type of graphs called power law graphs. In these realistic networks, the degree distribution follows the power law distribution, at least asymptotically. The fraction of nodes with degree k is proportional to the reciprocal of k power C where C is a constant named the exponential factor. The emergence of the power law distribution has changed the existing approaches to several optimization problems on networks. Institutively we can get faster algorithms solving a particular problem if we exploit all the properties of the problem as well as the type of networks. However, using the power law distribution in designing new algorithms is challenging and it requires new techniques and approaches. In other direction is to reevaluate the difficulty of the problem in this type of networks. Many problems are proved hard to be solved on general graphs but they may be easier to solve on power law graphs.

Objectives:

• Design faster algorithms to solve several optimization problems that exploit the power law distribution
• Revisit the hardness results of several problems on the new type of networks
• Re-analyze existing solutions on the new network models capturing the power law property